SCNN:一种卷积核的稀疏化方法以及CPU上的高效稀疏矩阵乘法
论文:Sparse Convolutional Neural Networks
作者:Baoyuan Liu, Min Wang, Hassan Foroosh, Marshall F. Tappen, Marianna Penksy
一作单位:Computational Imaging Lab, Computer Science, University of Central Florida, Orlando, FL, USA
录用情况:CVPR'2015
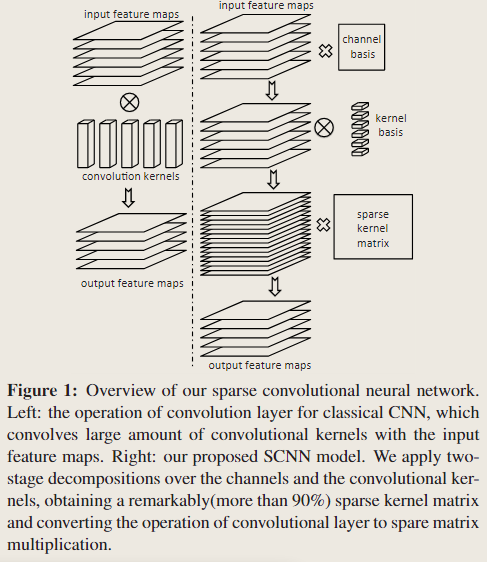
本文将卷积核两次分解,之后对第二次分解得到的“权重”矩阵进行稀疏化,对于ILSVRC2012数据集上训练的一个5层卷积层的网络,经过微调,在1%的性能损失下,获得了90%的稀疏率;尽管稀疏的算法在高度并行的GPU设备上并不吃香,但是对无GPU设备的加速仍有其意义,因此本文设计了在CPU上高效的稀疏矩阵乘法,获得了实质的推理加速;
方法
线性分解+稀疏化
记输入 \(I\in \mathbb{R}^{h\times w \times m}\),原来的卷积核为 \(K \in \mathbb{R}^{s\times s \times m \times n}\),输出为 \(O \in \mathbb{R}^{(h-s+1)\times(h-s+1)\times n}\) (stride=1, padding=0),作者将标准卷积表示为如下形式,计算复杂度为 \(O(s^2mn(h-s+1)^2)\)
\[ O(y, x, j) = \sum_{i=1}^m\sum_{u,v=1}^s K(u,v,i,j)I(y+u-1, x+v-1,i) \]
使用的第一种变换是对原卷积核 \(K\) 在通道维度上进行分解,得到 \(P\in \mathbb{R}^{m\times m}\) 和 \(R \in \mathbb{R}^{s\times s \times m \times n}\);这样有 \(O \approx R*J\);

第二种变换是继续将 \(R\) 进行线性分解,为第 \(i\) 个通道的 \(R(\cdot,\cdot, i, \cdot)\) 找到 \(q_i\) 个基 \(\mathcal{Q}_i\in \mathbb{R}^{s\times s\times q_i}\),与权重 \(\mathcal{S}_i\in \mathbb{R}^{q_i\times n}\) 的线性组合得到 \(R(\cdot,\cdot, i, \cdot)\)
用 \(\mathcal{T}_i \in \mathbb{R}^{(h-s+1)\times (h-s+1)\times q_i}\) 表示变换后的输入的第 \(i\) 的通道与第 \(i\) 组基进行卷积得到的 \(q_i\) 个中间结果:

将此中间结果再与权重进行线性组合得到输出:
\[ O(y, x, j) \approx \sum_{i=1}^m \sum_{k=1}^{q_i} \mathcal{S}_i(k, j) \mathcal{T}_i(y, x, k) \]
从 \(I\) 到 \(J\) 的变换需要 \(O(m^2hw)\) 的计算;
从 \(J\) 到 \(\mathcal{T}\) 需要 \(s^2(h-s+1)^2\sum_{i=1}^mq_i\) 的计算;
最后与权重线性组合的过程可以用单个 \((h-s+1)^2\times\sum_{i=1}^m q_i\) (变形 \(\mathcal{T}\)) 和 \(\sum_{i=1}^m q_i \times n\) (变形 \(\mathcal{S}\)) 矩阵乘法得到,而我们希望权重矩阵是稀疏的(\(\gamma\) 是密集度,即非零元素占比)并使用稀疏的矩阵乘法,这样最后的稀疏矩阵乘法计算复杂度为 \(O(\gamma n(\sum_{i=1}^mq_i)(h-s+1)^2)\);
综上,笔者得到总体的计算复杂度是: \[ (\gamma n + s^2)\left( \sum_{i=1}^m q_i \right ) (h-s+1)^2 + m^2hw \]
而原文中给的复杂度,将 \(i\) 上限错误写成了 \(n\);在 \(q_i < s^2\) 的条件下,\(\sum_{i=1}^m q_i < ms^2\),即我们给出的这个复杂度比原文的复杂度更“紧”;而原文的写法也更好与原卷积的计算复杂度进行比较;

不过原文对 \(i\) 的上限错误也导致其接下来的另一个小错误:与原复杂度 \(mns^2(h-s+1)^2\) 对比,希望现在的复杂度优势项是 \(\gamma mns^2(h-s+1)\)(\(\gamma\) 决定了加速比),另外两项就要相比于优势项可忽略,即 \(\sum_{i=1}^m q_i = m\overline{q} < \gamma mn\) (原文写的是 \(\overline{q} <\gamma m\)),还有 \(m \ll \gamma ns^2\);
综上,要想在理论上对算法复杂度有改进,需要满足:
\[ \left\{ \begin{matrix} q_i < s^2\\ \overline{q} < \gamma n\\ m < \gamma ns^2 \end{matrix} \right. \]
如果了解论文Speeding up Convolutional Neural Networks with Low Rank Expansions,就会发现这里使用的kernel basis线性组合的方法与该论文的scheme1分解方法基本一致,这里在之前添加了channel basis,没有把kernel basis进一步做成可分离的,并且对于每个通道使用不同数量的kernel basis;
参数学习
接下来的问题就是,如何学习 \(P\), \(Q_i\), \(S_i\) (\(i = 1, \dots, m\)),并且让 \(S_i\) 是稀疏的?
总体步骤分为初始化和微调,在初始化阶段主要获得合适的 \(P\), \(Q_i\), \(S_i\),使得重建误差很小,但是此时的稀疏性并不好;在微调阶段使用分类损失+稀疏正则项,对 \(S_i\) 进行稀疏化;
初始化
对 \(K\) 在 通道方向分解得到 \(R\), \(P\);对 \(R(\cdot, \cdot, i, \cdot)\) 在个数方向上分解得到 \(S_i\), \(Q_i\);这两种高维张量的分解都可以通过reshape转化为矩阵分解问题,因而有三种初始化方法:
- 使用字典学习算法(本文作者指出该优化是非凸的且在精度和稀疏度上有中和);
- 使用主成分分析;
- 初始化 \(P\) 和 \(Q_i\) 为单位标准基:那么令 \(R=K\) 即可以使得 \(K(u,v,i,j) = \sum_{k=1}^m R(u, v, k, j)P(k,i)\);不过,\(S_i\) 与 \(R(\cdot, \cdot, i, \cdot)\) 的维度不一致,如果 \(q_i \ge n\),可以通过构造在初始化时使得 \(R(u,v,i,j) = \sum_{k=1}^{q_i} S_i(k,j)Q_i(u,v,k)\),反之若 \(q_i < n\),则不能;
微调
微调阶段作者主要希望在保持性能的前提下增加 \(S_i\) 的稀疏度,设计目标函数如下: 
稀疏化与低秩化的区别
设 \(M \in \mathbb{R}^{m\times n}\),\(S \in \mathbb{R}^{m\times n}\),\(P\in \mathbb{R}^{n \times n}\),有矩阵分解 \(M=SP\);对 \(S\) 进行稀疏化,相当于增多 \(S\) 的零元素个数;对 \(S\) 进行低秩化,相当于增加 \(S\) 的零列(可以由其他列线性组合得到的列);
从性能上看,稀疏化比起低秩化损失更小;从速度上看,低秩化是结构性的,稀疏化是非结构性的,前者更便于使用现有的算子高效实现达到实际的加速目的;
稀疏的矩阵乘法
作者利用推理时模型的如下两个事实:
- 与卷积核相关的稀疏矩阵不再改变;
- 输入不是稀疏的;
在OpenBLAS上实现了一种密集卷积与稀疏卷积的算法:
对于每一个子块的乘法,\(C=A\times B\),其中 \(A\in \mathbb{R}^{8\times k}\),\(B\in \mathbb{R}^{k\times 8}\),8是当时作者使用的AVX指令集最大可以并行计算的float的数量;在密集乘法中,\(C\) 的一列可以看作是 \(A\) 的一列与 \(B\) 的对应列的加权和;假设 \(A\) 是密集的,\(B\) 是稀疏的,作者通过寻找 \(B\) 中非零元素的位置,按照 \(B\) 的行列顺序,重新生成了乘法计算的代码,如下图所示:

线性层的稀疏化
可以将线性层权重分解为密集矩阵与稀疏矩阵的乘法,并选择稀疏化维度更大的那个矩阵,为了使得密集矩阵更小;
实验
在对分类模型稀疏化时,作者首先拿到已训练好的权重,之后按照前文方法修改卷积计算,进行初始化+微调,并应用阈值函数来获得稳定的稀疏;在收敛之后,去除稀疏限制(但保留阈值函数)再微调一阵以达到最佳精度;
作者在实验中比较了微调后卷积核与原来卷积核的相似度,发现从conv1到conv3,这种相似度从0.85下降到0.34,而精度没有太大损失,说明没有必要逐个卷积核地恢复,基于分类损失的全局微调很有效;
作者还比较了对基的三种初始化方式,发现他们在性能上没有显著差异,但PCA的初始化,微调后得到的稀疏度最高;接着作者发现,稀疏度与主成分有很强的相关性,越重要的成分越容易稀疏;
更多实验详见原文。
