字典学习卷积模块以加速网络推理
论文:LCNN: Lookup-based Convolutional Neural Network
作者:Hessam Bagherinezhad, Mohammad Rastegari, Ali Farhadi
一作单位:University of Washington, XNOR.AI
录用情况:CVPR'2017
本文将卷积运算替换为学习一个字典和一组线性组合的权重,并提出了直接从头开始训练的方式,除了一般的分类实验,本文还证明了这种方法在few shot learning的提升,以及对网络初始迭代时收敛水平的提升等;在AlexNet的架构上的修改,该方法获得了55.1%的ImageNet top1准确率以及3.2倍的加速比;
方法
在不同卷积核之间、不同空间位置上建立共享的字典
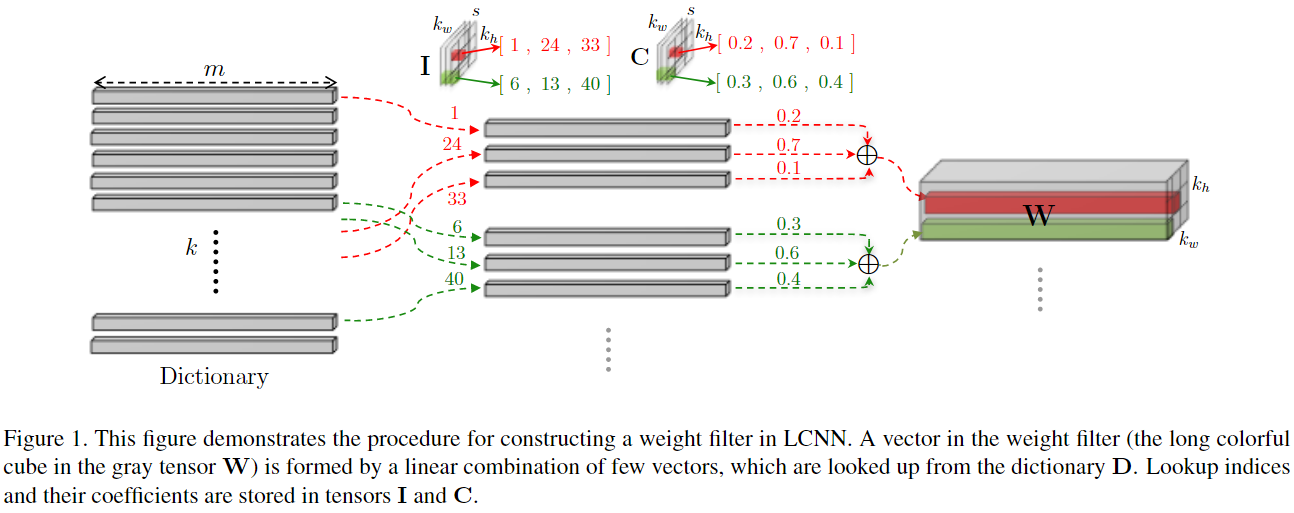
本文将 \(n\) 个 \(m\times k_w\times k_h\) 的视为 \(nk_wk_h\) 个长度为 \(m\) 的向量,并希望学习一个的字典 \(D\in\mathbb{R}^{k\times m}\),以及在每个 (t, r, c) 位置使用的 \(s\) 个字典向量索引 \(I_{[t,r,c]}\) 和对应的权重 \(C_{[t,r,c]}\),从而能够将一个卷积 \(W\in \mathbb{R}^{m\times k_w\times k_h}\) 的 \(r\) 行 \(c\) 列的权重表示为如下字典向量的线性组合的形式:
\[ W_{[:, r, c]} = \sum_{t=1}^s C_{[t,r,c]} \cdot D_{[I_{[t,r,c]},:]} \quad \forall r, c \]
为了将这种表示下的卷积核应用到卷积计算中(在卷积运算中拆出 \(W_{[:, r, c]}\) 一项),作者从卷积核每个位置与输入做了怎样的运算的视角来看,整个卷积相当于输入与这些位置上卷积向量做1x1卷积后,经过位置相关的偏移操作,将结果求和;表达为如下形式:
\[ \begin{split} X*W &= \sum_{r,c}^{k_h, k_w}\operatorname{shift}_{r,c}(X * W_{[:, r, c]})\\ &= \sum_{r,c}^{k_h, k_w}\operatorname{shift}_{r,c}(X * (\sum_{t=1}^s C_{[t,r,c]} \cdot D_{[I_{[t,r,c]},:]}))\\ &= \sum_{r,c}^{k_h, k_w}\operatorname{shift}_{r,c}(\sum_{t=1}^s C_{[t,r,c]} (X * D_{[I_{[t,r,c]},:]}))\\ &= \sum_{r,c}^{k_h, k_w}\operatorname{shift}_{r,c}\left(\sum_{t=1}^s C_{[t,r,c]} S_{I_{[t,r,c]}}\right )\\ \end{split} \]
这意味着,对于共享同一个字典中的同一个层的所有卷积,我们可以先计算出 \(X\) 与字典中所有向量的1x1卷积结果 \(S_{[i,:,:]}=X*D_{i,:}\),之后只需要索引到需要的结果,加权求和,放到需要的位置即可;
至此,只要 \(s\), \(k\) 设置得当,理论上计算量相比原来的卷积运算已经大大减少;
但是,我们关心的第一个问题是,如何将索引、加权和以及shift的过程向量化,从而极大地利用现有的高度并行化的算子,从而真正提升前向传播速度?
第二个问题是,在使用了向量化的算子之后,并应用了其默认的梯度下降优化,那么如何在优化过程中建立并保持稀疏性? (\(s\ll k\))
训练LCNN
利用如下事实:
假设 \(T\in \mathbb{R}^{k\times k_w\times k_h}\) 是独热张量,只在 \(T_{[t,r,c]}=1\),其余位置均为0,那么有 \(S*T = \operatorname{shift}_{r,c}(S_{[t,:,:]})\);
我们可以在前向传播过程中学习一个稀疏张量 \(P\in\mathbb{R}^{k\times w\times h}\),其中,\(P_{[:,r,c]}\) 表示了在r,c位置的稀疏权重:
\[ P_{j,r,c} = \left \{ \begin{matrix} C_{t,r,c}, &\exists t: I_{t,r,c} = j\\ 0, &\text{otherwise} \end{matrix} \right . \]
这样一来,我们可以使用卷积来表示索引、加权和、偏移求和的过程,下式和图二说明了这一点:
\[ \begin{split} X*W &= \sum_{r,c}^{k_h, k_w}\operatorname{shift}_{r,c}\left(\sum_{t=1}^s C_{[t,r,c]} S_{I_{[t,r,c]}}\right )\\ &= \sum_{r,c}^{k_h, k_w}\operatorname{shift}_{r,c} (S * P_{[:,r,c]})\\ &= S*P \end{split} \]

并且,如果我们能够在训练时得到稀疏的 \(P\),就可以通过寻找非零元素的方式得到 \(I\) 和 \(C\),用于高效的推理;
接下来,作者通过添加正则项使得 \(P\) 稀疏,按照对 \(P\) 的定义,应该有 \(\lVert P_{[:,r,c]}\rVert _{\mathcal{L}_0} = s\);但是 \(\mathcal{L}_0\) norm(非零元素的数量)是不连续的函数,不可导,因此作者将 \(P_{[:,r,c]}\) 的从大到小排列后,第 \(s\) 个之后的元素记为0,并计算 \(\mathcal{L}_1\) norm(元素绝对值之和);期望通过将前 \(s\) 个元素的绝对值变小,来让被在zero out的那部分元素很接近0;
至此并没有完全达到稀疏化的目的,因为当 \(P_{[t,r,c]}\) 缩小到0时,其梯度不一定为0,这样在下一次迭代过程中其绝对值又会变大;
我们可以为 \(P\) 包裹一层阈值函数,当 \(|P_{[t,r,c]}|\) 的值小于 \(\epsilon\) 时,该位置直接置0,意味着回传的梯度也是0,那么这里就永远保持在0;
Few-shot learning
对于普通的CNN,将预训练的模型的分类头替换成没有任何先验知识的分类头(参数量很多,容易过拟合),对少样本的类别进行学习;
对于LCNN,可以使用预训练模型分类层的字典,因此只用学习权重和索引,且对于其他层,可以固定索引,只微调权重;
Few-iteration learning
浅层网络学习到的字典 \(D\in\mathbb{R}^{k\times m}\),可以与通道数为 \(m\) 的深层网络共享;加速在段周期内的收敛过程;
实验
通过调整字典大小 \(k\),正则化参数 \(\lambda\) 和阈值 \(\epsilon\) 来调整模型学习后的稀疏率,从而调整推理时加速比;
s 是间接调整的
每一层的阈值和正则化参数与该层初始化方差成正比,是为了让每层的系数水平相近;
对于第一层而言,由于输入通道是3通道的(字典向量长度为3)因此字典最多只需要3个向量(再多就一定有线性相关了);
对于线性层,将其视为1x1卷积后,输入通道比较大,因此字典大小也很大;其他层的字典大小作者凭借经验设定一组候选值进行实验;
实验结果与分析详见原文;
总结
基于本文的工作,笔者有一些朴素的思考:
本文通过将传统卷积视为1x1卷积结果的shift和,认为这 \(nk_wk_h\) 个 \(\mathbb{R}^m\) 空间的卷积向量可以表示为 \(\mathbb{R}^k\) 子空间的坐标(字典向量是基,权重是坐标),该过程利用了输入 \(m\) 个通道的冗余性;接着,作者假设,这些坐标是稀疏的,每个坐标的非零元素不超过 \(s\) 个,这些利用的是 \(nk_wk_h\) 个向量的表示可以划分到 \(\begin{pmatrix} nk_wk_h\\s \end{pmatrix}\) 个簇中,这样一看,我们似乎可以找到一种从已经训练好的卷积核初始化字典的方法:
- 找到卷积核的低维投影(如PCA等);
- 在低维空间使用聚类,并限制这些类中心坐标是稀疏的;
在此之前,需要验证一下本文得到的字典的秩是否为 \(k\)?关于2中提到的聚类中心坐标稀疏的限制如何实现?以及,我们是否可以换别的维度进行第1步的降维?
机器学习中有个经典方向:字典学习,笔者应该回去补一补了;
