卷积分解：考虑非线性函数、多层误差累积以及秩选择

发表于 2023-01-13 更新于 2023-02-12 分类于论文阅读阅读次数：

论文：Efficient and Accurate Approximations of Nonlinear Convolutional Networks

作者：Xiangyu Zhang, Jianhua Zou, Xiang Ming, Kaiming He, Jian Sun

一作单位：Microsoft Research

录用情况：CVPR'2015

作者从卷积核沿着空间维度和通道维度展开后的低秩性入手，将其分解为更少的卷积核以及一系列1x1卷积；接着，作者考虑了卷积核后的非线性层的印象，设计了一个更加复杂的优化目标，并给出了优化算法；作者还考虑了多层误差累积现象，将优化目标改为“反对称”的；对于每一层的秩的选择，作者将其视为一个组合问题，用贪心法求解；在这一系列的策略下，SPPnet在字符分类精度损失0.7%的情况下获得了4.5倍加速比；

方法

响应的低秩估计

卷积层的输入时低秩的，卷积核是低秩的，那么输出（响应）也应到是低秩的；我们向来都是利用这种低秩性，来减小计算复杂度；

设一个卷积核的尺寸为 \(k\times k\times c\)，一个输入表示为 \(\mathbf x \in \mathbb{R}^{k^2c+1}\)（补充了1，用于与偏置项相乘），输出响应 \(\mathbf y\in \mathbb{R}^d\) 由下式计算出：

\[ \mathbf y = W\mathbf x \]

其中，\(W \in \mathbb{R}^{d\times(k^2c+1)}\)，\(d\) 是卷积核的个数，每个卷积核沿着空间和通道维度展平并append上了偏置项，该式的复杂度是 \(O(dk^2c)\)；

如果向量 \(\mathbf{y}\) 可在低秩空间中表示，记 \(\overline{\mathbf{y}}\) 是其均值，存在 \(M \in \mathbb{R}^{d\times d}\)，\(\operatorname{rank}M = d' < d\)，使得： \[ \mathbf{y} = M(\mathbf{y} - \overline{\mathbf{y}}) + \overline{\mathbf{y}} \]

笔者暂时不能清晰地说出这条引理为什么是对的；

将上式展开，得到：

\[ \mathbf{y} = MW\mathbf{x} + \mathbf{b} \]

其中 \(\mathbf{b} = \overline{\mathbf{y}} - M \overline{\mathbf{y}}\)；

对于低秩矩阵 \(M\) 我们可以将其分解为 \(P, Q\in\mathbb{R}^{d\times d'}\)，即 \(M=PQ^T\)，记 \(W' = Q^TW\)，那么有

\[ \mathbf{y} = PW'\mathbf{x} + \mathbf{b} \]

该式的复杂度是 \(O(d'k^2c + dd')\)，由于通常有 \(dd'\ll d'k^2c\)，那么可以将理论复杂度减少到原来的约 \(d'/d\)；

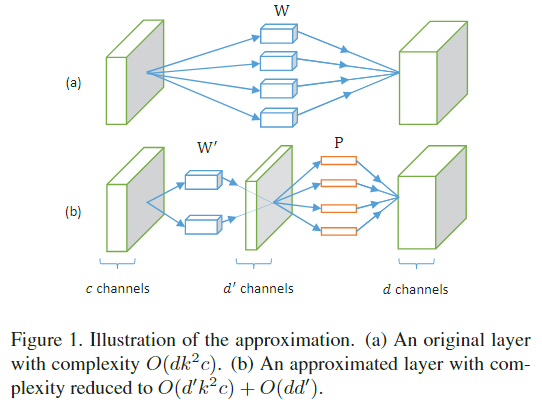
在实现中，\(W'\) 相当于 \(d'\) 个 \(k\times k \times c\) 卷积核，\(P\) 相当于 \(d\) 个 \(1\times 1\times d';\) 个卷积核，如图1所示；

对 \(M\) 的低秩分解可以用多种方法实现，奇异值分解，主成分分析，都是如下目标函数的解：

\[ \begin{split} \min_{M} &\sum_i\Vert (\mathbf{y}_i - \overline{\mathbf{y}}) - M(\mathbf{y}_i - \overline{\mathbf{y}})\Vert_2^2 \\ \text{s.t.}~ &\operatorname{rank}M \le d' \end{split} \]

考虑非线性层

以ReLU作为非线性函数为例，对于 \(\mathbf{y}_i\) 的非负部分的准确估计很重要，而对于其负数部分有再大的估计误差也不会继续传播；因此，在理想情况下，最小化重建损失问题应该记为：

\[ \begin{split} \min_{M,\mathbf{b}} &\sum_i \lVert r(\mathbf y_i) - r(M\mathbf{y}_i + \mathbf{b}_i) \rVert _2^2\\ \text{s.t.}~ &\operatorname{rank}M\le d' \end{split} \]

由于低秩约束以及非线性函数的存在，该问题并不好解，作者将问题relax为了如下形式：

\[ \begin{split} \min_{M,\mathbf{b}, \{\mathbf{z}_i\}} &\sum_i \lVert r(\mathbf{y}_i) - r(\mathbf{z}_i) \rVert _2^2 + \lambda \lVert \mathbf z_i - (M\mathbf{y}_i + \mathbf{b}_i) \rVert _2^2\\ \text{s.t.}~ &\operatorname{rank}M\le d' \end{split} \]

该问题在 \(\lambda\rightarrow\infty\) 时，逼近前一个问题；对于该问题，可以交替优化 \(\{\mathbf{z}_i\}\) 和 \(M,\mathbf{b}\)；

具体的优化方法见原论文，此处不再赘述；

考虑多层误差累积

使用逐层优化的方式，我们提前保存下标准网络各层的输入；记在估计的网络中当前层的输入为 \(\hat{\mathbf{x}}\)，在精确的网络中当前层的输出为 \(\mathbf{x}\)，优化问题可写为：

\[ \begin{split} \min_{M,\mathbf{b}, \{\mathbf{z}_i\}} &\sum_i \lVert r(W\mathbf{x}_i) - r(\mathbf{z}_i) \rVert _2^2 + \lambda \lVert \mathbf z_i - (MW\hat{\mathbf{x}}_i + \mathbf{b}_i) \rVert _2^2\\ \text{s.t.}~ &\operatorname{rank}M\le d' \end{split} \]

相比于都使用 \(\hat{\mathbf{x}}\) 或者都使用 \(\mathbf{x}\)，这种设计更合理；

各层秩的选择

每一层的 \(d'\) 应该是多少最合适？这里要兼顾精度与速度；在速度上，前文我们得到本文的分解方法在将每层的计算复杂度缩小到原来的 \(d'/d\)，即第 \(l\) 层原来的复杂度为 \(C_l\)，期望压缩后整个网络的复杂度为 \(C\)，要对整个网络有加速，至少要满足 \(\sum_l \frac{d'}{d}C_l \le C\)；

作者还通过实验发现，仅压缩一层，精度水平与PCA能量水平大约是线性关系，因此，可以用各层保存的能量（保留的特征值的和）的积来指示整个网络的精度水平，因此，优化问题为：

\[ \begin{split} \max_{\{d_l'\}}~ &\mathcal{E} = \prod_l \sum_{a=1}^{d_l'}\sigma_{l,a}\\ \text{s.t.}~ &\sum_l \frac{d'}{d}C_l \le C \end{split} \]

使用如下的贪心方法优化：

初始化集合 \(\{\sigma_{l,a}\}\)，初始化 \(d_l'=d_l\)；
每次从集合中剔除一个 \(\sigma_{l, d_l'}\)，即将第 \(l\) 层去除特征值最小的对应的特征向量方向，这将复杂度降低了 \(\Delta C = \frac{1}{d_l}C_l\)，也将目标函数减少为原来的 \(\Delta \mathcal{E}/\mathcal{E} = \sigma_{l,d'}/\sum_{a=1}^{d_l'}\sigma_{l,a}\)，希望对前者的减少大于对后者的减少，因此遍历所有层，找到使得 \(\frac{\Delta \mathcal{E}/\mathcal{E}}{\Delta}\) 最小的那个 \(\sigma_{l, d_l'}\) 并剔除；
直到达到期望的复杂度 \(C\) 为止；

实验

通过逐层压缩实验，证明了非线性压缩在Conv2-7层上都对线性压缩有更低的分类误差；

通过整个网络的实验，证明了非对称的优化目标比对称的优化目标有更低的分类误差；相同加速比下，使用rank selection相比于手工设置的一组rank，也能降低分类误差；

得益于非对称目标函数的设计，可以在对某一层压缩时使用多种方法，得到的结果会作为下一层压缩时的输入，而下一层重建目标仍然是精确网络上的输出响应；