度量空间与连续性
前几日接触到一个新概念,Lipschitz Constant,本文是笔者在Wikipedia上递归搜索归纳的部分数学公里、定义、例子;抽象代数与拓扑几何的部分暂不在本文讨论;笔者不是数学专业,因此逻辑与表达多有不严谨之处,还请多多指正;
度量空间 (Metric space)
定义
对于一个集合\(M\)中的两个元素,可以给出一种度量\(d\),称为度量空间,记作\((M,d)\),也是一个函数:\(d:M\times M \rightarrow \mathbb{R}\):
跳出直观的欧几里得距离,度量是一种抽象的、隐喻的概念,又是也可以理解为从一个点到另一个点需要花费的成本;
对于任意的\(x,y,z\in M\),度量空间满足下面4条公理,
- \(d(x,x)=0\)
- 如果\(x\ne y\),则\(d(x,y)>0\)
- \(d(x,y)=d(y,x)\)
- \(d(x,z)\le d(x,y) + d(y, z)\)
常见的距离函数有:欧几里得距离\(d_2\),曼哈顿距离\(d_1\),切比雪夫距离\(d_{\infty}\),球面距离,汉明距离等等,并且有: \[ d_\infty(p,q)\le d_2(p,q) \le d_1(p,q) \le 2d_\infty(p,q) \]
子空间
度量空间\((M,d)\),有\(A\subseteq M\),则\(A\)的诱导度量\(d_A:A\times A\rightarrow \mathbb{R}\)定义为 \[ d_A(x,y)=d(x,y) \] 球面集合\(S^2\)是\(\mathbb{R^3}\)的子集,球面上的诱导度量是3维空间中的欧几里得距离;
收敛性
这里先给出欧式空间上的表述,可以推广到度量空间:
一个数列\((x_n)\)收敛到\(x\),当且仅当对于任意的\(\epsilon>0\),存在整数\(N\),对于所有的\(n>N\)都有\(d(x_n,x)< \epsilon\);
完备性 (completeness)
直观地说,如果没有“缺失点”,即任何看起来收敛的序列(随着叙述的增加愈发靠近),确实都是收敛的,则称该度量空间是完备的;
一个数列\((x_n)\)是\((M,d)\)中的柯西数列,当且仅当对于任意的\(\epsilon>0\),存在整数\(N\),对于所有的\(m,n>N\)都有\(d(x_m,x_n)<\epsilon\);
收敛数列一定是柯西数列,(如果\(x_m\)与\(x_n\)与极限的距离都不超过\(\epsilon\),则通过三角不等式推出相同条件(\(N\))下\(x_m\)与\(x_n\)的距离不超过\(2\epsilon\);
如果度量空间中所有的柯西数列都是收敛的,则度量空间是完备的;
例如,区间\((0,1)\)不完备而\([0,1]\)完备,有理数集不完备而实数集完备;
有界性 (bounded)
在\(M\)中存在一个距离上届,称为\(M\)的直径;
完全有界(or precompact),定义涉及拓扑;
紧凑性 (compactness)
有几个紧凑性的等价定义,这里忽略涉及到拓扑概念的:
- 每一个数列都有一个收敛的子数列;
- 完备的且完全有界的;
度量空间之间的映射
从度量空间到度量空间,有时称映射(maps)、有时称函数(functions)
等距映射 (Isometries)
一个函数\(f:M_1\rightarrow M_2\)是等距的,如果对于\(M_1\)中任意的点都有: \[ d_2(f(x),f(y))=d_1(x,y) \]
\(f\)应该是二元组到二元组的函数,上述\(f(x)\)理解为\(f(x,y)\)的第一项,\(f(y)\)是第二项
例如\(f:(\mathbb{R}^2,d_1)\rightarrow(\mathbb{R}^2,d_\infty)\)有: \[ f(x,y)=(x+y,x-y) \] 因为\(|x|+|y|=\max({|x+y|,|x-y|})\)
连续映射(continuous maps)
存在多种等价的定义,其中\(\epsilon-\delta\)定义为:
一个函数\(f:M_1\rightarrow M_2\)是连续的,如果对于\(M_1\)中任意的点\(x\),和任意的\(\epsilon > 0\),都有\(\delta > 0\)使得对于\(M_1\)中任意的\(y\)有: \[ d_1(x,y)<\delta \Rightarrow d_2(f(x),f(y))<\epsilon \]
一致连续映射(uniformly continuous maps)
一个函数\(f:M_1\rightarrow M_2\)是一致连续的,如果对于任意的实数\(\epsilon > 0\),存在\(\delta >0\)使得对于\(M_1\)中任意的点\(x,y\)满足\(d(x,y)<\delta\)的,有 \[ d_2(f(x),f(y))<\epsilon \]
在连续的定义中,\(\epsilon\)是\(x\)和\(\delta\)的函数;在一致连续的定义中,\(\epsilon\)仅是\(\delta\)的函数;后者的条件更强;
李普希兹映射 (Lipschitz maps)
经过这种映射,距离的拉伸不会超过一个上界:给定一个实数\(K>0\),函数\(f:M_1\rightarrow M_2\)是K-Lipschitz映射当: \[ d_2(f(x),f(y))\le Kd_1(x,y) \] 特殊地,当\(K<1\)时称为收缩(contraction)
准等距映射(Quasi-isometries)
函数\(f:M_1\rightarrow M_2\)是准等距映射当存在常数\(A\ge 1\)且\(B\ge 0\)有: \[ \frac{1}{A}d_2(f(x),f(y))-B\le d_1(x,y) \le Ad_2(f(x),f(y))+B \]
李普希兹连续
上文中的李普希兹映射的定义也是李普希兹连续的定义,其中\(K\)是李普希兹常量,最小的\(K\)称为the best Lipschitz constant或者dilation。
一种特殊情况是当\(f\)是实函数时,上述定义相当于限制了函数在其定义域上任意两点的割的绝对值存在上限\(K\):
\(|f(x_1)-f(x_2)|\le K|x_1-x_2|\)
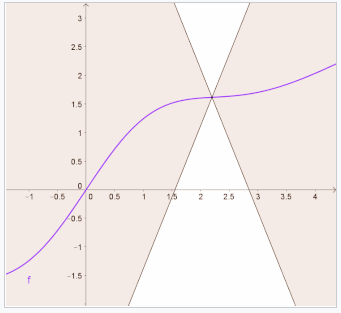
如上图所示,无论怎么移动,两条斜率绝对值为\(K\)的斜线割开的上下部分均不会有\((x,f(x))\),即满足李普希兹连续条件
在神经网络中,我们假设模型函数具有一个小于1的李普希兹常量,通常是为了避免梯度传播过程中发生数值问题;
